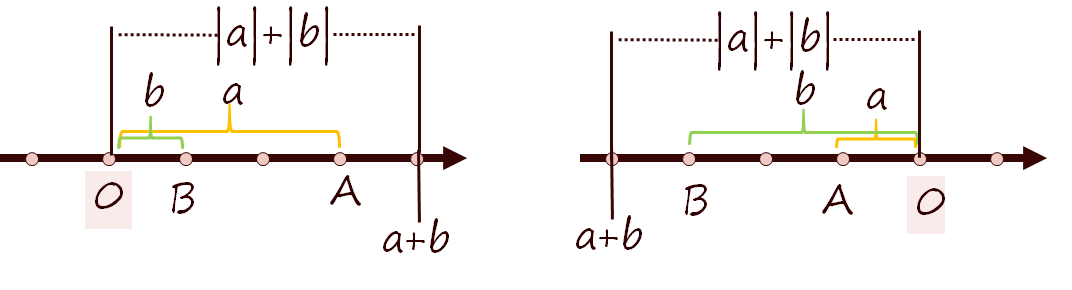不等式和绝对值不等式

不等式

从几何图形中看

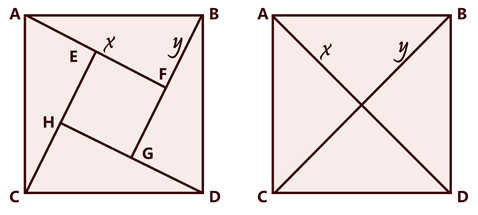
下图左边，一个正方形中划分出四个直角三角形。设每个三角形的长边为$x$，短边为$y$，那么整个正方形的边长就是$\sqrt{x^2+y^2}$。整个正方形的面积大于四个直角三角形的面积，即$x^2+y^2>2xy$。

右边的图就是将直角三角形改为等腰直角三角形，此时EFGH已经合并成一个点，此时整个正方形的面积等于四个等腰直角三角形的面积，即$x^2+y^2=2xy$。

综上所述可以推导出定理1：

$x^2+y^2 \geqslant 2xy ,当且仅当x=y时等号成立$

从代数公式直接推导

$\because (x-y)^2 \geqslant 0$

$\therefore x^2 + y^2 - 2xy \geqslant 0$

$\therefore x^2 + y^2 \geqslant 2xy$

令$x=\sqrt a,y=\sqrt b$，上边公式就可以写为定理2，基本不等式：

$\frac{a+b}{2} \geqslant \sqrt{ab} ,当且仅当x=y时等号成立$

对于正数a、b，我们通常把$\frac{a+b}2$称为算数平均（arithmetic mean），把$\sqrt {ab}$称为几何平均（geometric mean）。

因此基本不等式可以表述为两个正数的算数平均大于等于它们的几何平均

由上边我们还可以推广得到定理3：

对于n个正整数$a_1$、$a_2$…$a_n$，它们的算数平均值不小于它们的几何平均值。

$\frac{a_1+a_2+...+a_n}{n} \geqslant \sqrt{a_1 a_2 ... a_n} ,当且仅当a_1=a_2=...=a_n时等号成立$

绝对值不等式

从几何上看

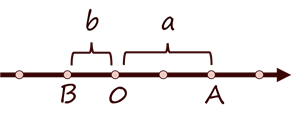
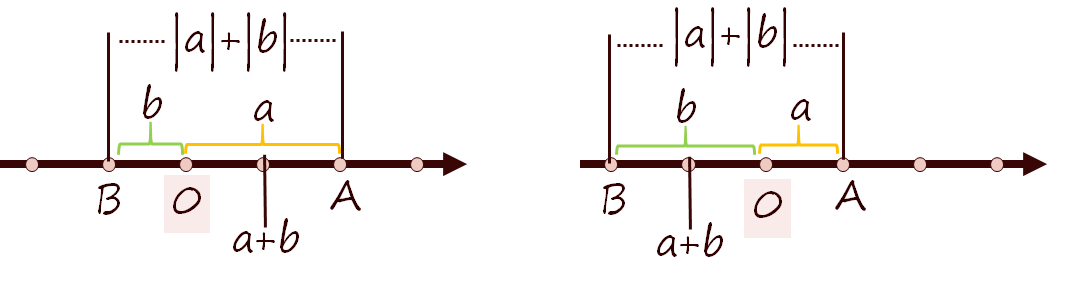
在一个坐标轴上$|a|$代表的是A点到原点O的距离，$b$代表B点到原点O的距离。

此外我们还可以知道$|b-a|或|a-b|$代表的是A、B两点之间的距离。

下边我们分情况讨论一下$|a+b|$：

• 当ab>0时，A、B位于原点的同一侧

  在坐标轴上表示出$|a|$、$|b|$、$|a+b|$，可以看出当两点位于原点的同一侧时，$|a|+|b|=|a+b|$

  

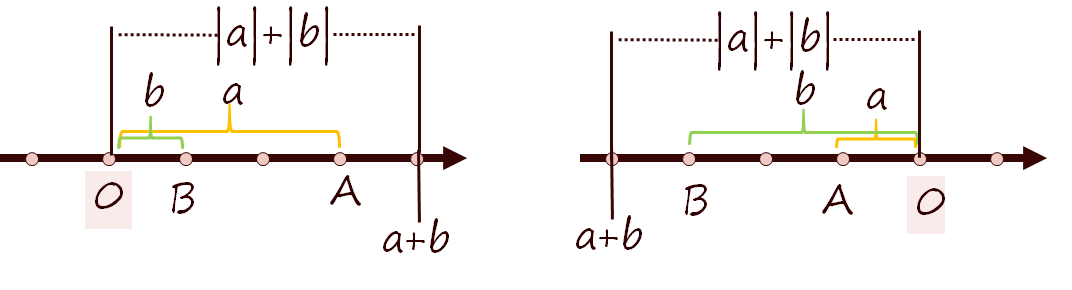
• 当ab<0时

  在坐标轴上表示出$|a|$、$|b|$、$|a+b|$，可以看出当两点位于原点的两边时，$|a|+|b|>|a+b|$

  

• 当ab=0时也是$|a|+|b|=|a+b|$

综上所述我们可以知道定理1-1：

$|a|+|b|\geqslant |a+b|，当且仅当ab\geqslant 0时等号成立$

从代数公式直接推导

$当ab\geqslant0时ab=|ab|$

$\begin{aligned}|a+b| &=\sqrt{(a+b)^{2}} \\ &=\sqrt{a^{2}+2 a b+b^{2}} \\ &=\sqrt{|a|^{2}+2|a b|+|b|^{2}} \\ &=\sqrt{(|a|+|b|)^{2}} \\ &=|a|+|b| \end{aligned}$

$当ab<0时ab=-|ab|$

$\begin{aligned}|a+b| &=\sqrt{(a+b)^{2}} \\ &=\sqrt{a^{2}+2 a b+b^{2}} \\ &=\sqrt{|a|^{2}-2|a b|+|b|^{2}} \\ &<\sqrt{a^{2}+2|a b|+b^{2}} \\ &=\sqrt{|a|^{2}+2|a b|+|b|^{2}} \\ &=\sqrt{(|a|+|b|)^{2}} \\ &=|a|+|b| \end{aligned}$

$\therefore |a|+|b|\geqslant |a+b|$

使用上述方法还可以看看$|a-b|$与$|a|-|b|、|a|+|b|$的关系，只看$|a|>|b|$的情况即可，因为下表中可以看出$|a|<|b|$没有太大的讨论意义。

列了个表

上图右半部分的表格可以看出

$|a|-|b| \leqslant|a-b| ，当且仅当ab\geqslant 0时等号成立$

$|a-b| \leqslant|a|+|b|，当且仅当ab\leqslant 0时等号成立$

综上可以推出定理1-2：

$|a|-|b| \leqslant|a-b| \leqslant|a|+|b|，当且仅当ab=0时等号成立$

还有一个表：

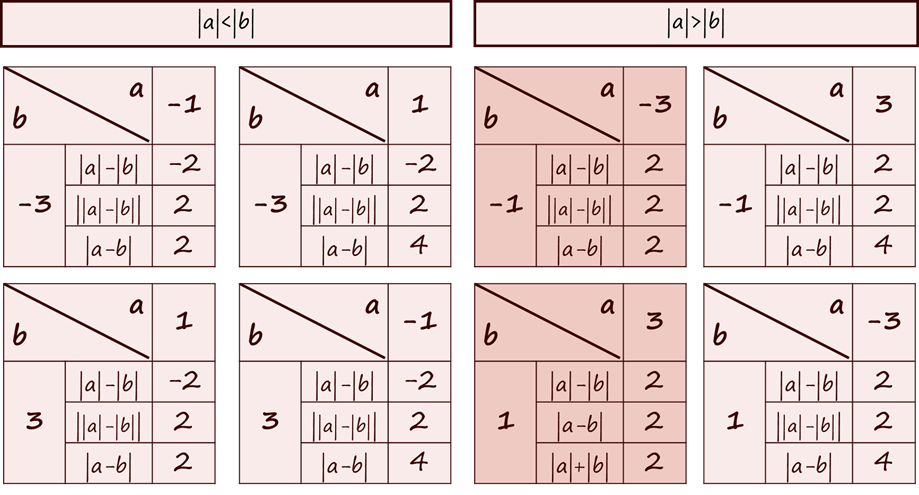
可以推出定理1-3：

$|a|-|b| \leqslant||a|-|b|| \leqslant|a-b|，当且仅当ab\geqslant 0时等号成立$

还可以推广得到定理2：

对于实数a、b、c，

$|a-c| \leqslant|a-b|+|b-c|，当且仅当(a-b)(b-c) \geqslant 0等号成立$