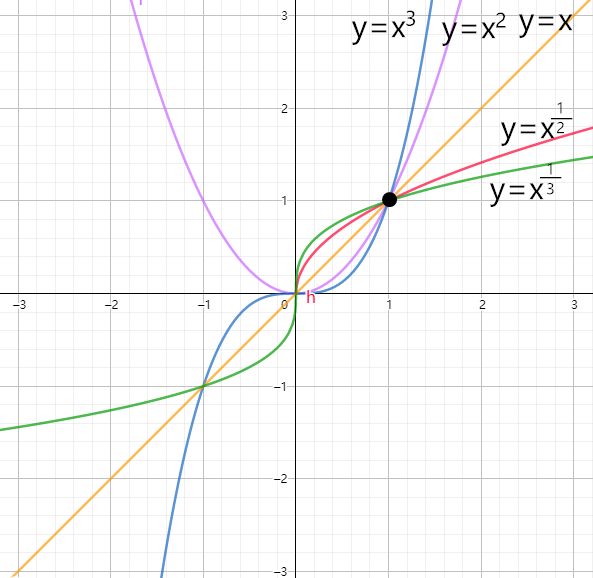基本初等函数

幂函数

$y= x^a (a为实数)$

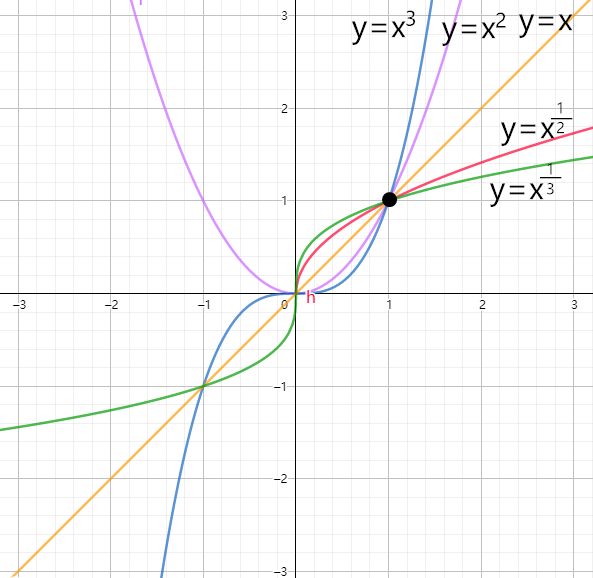
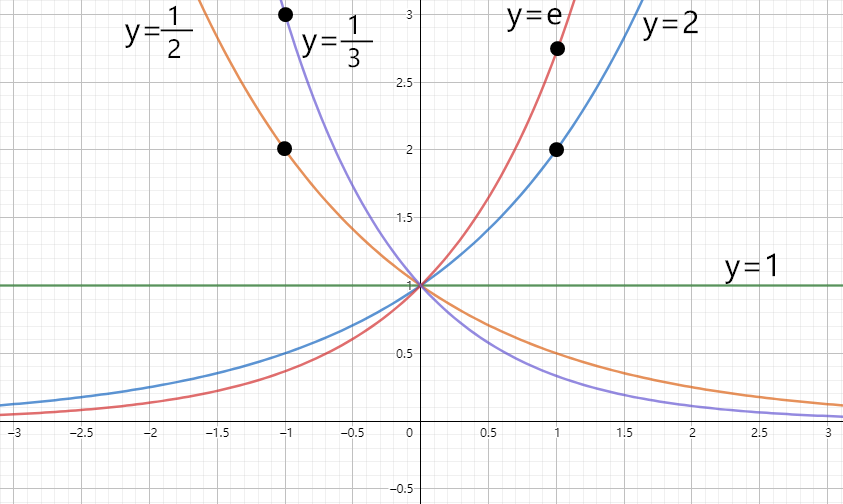
指数函数

$y=a^x(a>0 , a\neq 1)$

• 运算性质
  $a^r a^s =a^{r+s}(a>0, r, s \in Q)$

  $(a^r)^s=a^{rs}(a>0, r, s \in Q)$

  $(a b)^{r}=a^{r} b^{r}(a>0, b>0, r \in Q)$

• 其他

  • 平方
    $(a+b)^2=a^2+2ab+b^2$
    $a^2-b^2=(a+b)(a-b)$

  • 立方
    $a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)$
    $a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$
    $(a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}$

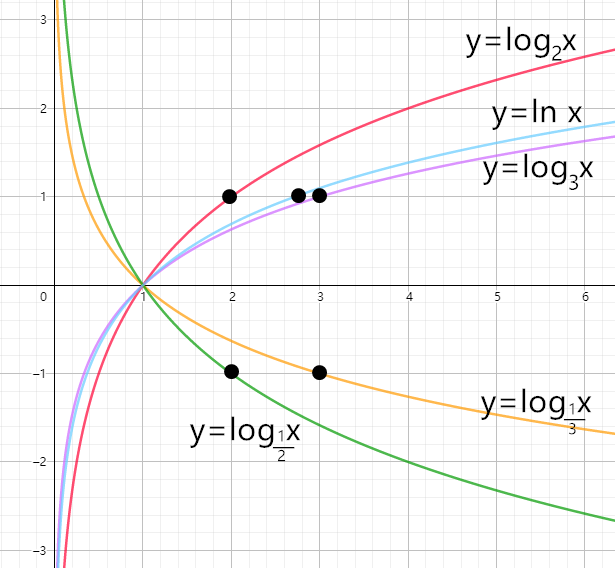
对数函数

$y=log_a^x (a>0,a\neq 1)$

• 指数和对数的交换
  当 $a>0, a \neq 1$ 时， $a^x = N \Leftrightarrow x=\log_a N$

• 运算性质
  如果 $a>0,$ 且 $a \neq 1, M>0, N>0,$ 那么:

  $a^{\log_a N}=N$

  $a^b=e^{b \ln a}$

  $\log_{a}(M \cdot N)=\log_{a} M+\log_{a} N$

  $\log_{a} \frac{M}{N}=\log _{a} M-\log_{a} N$

  $\log_{a} M^{n}=n \log_{a} M \quad(n \in \mathbf{R})$

  $\log_{a^n} N=\frac{1}{n} \log_{a} N (n \neq 0)$

• 换底公式
  $\log _{a} b=\frac{\log _{c} b}{\log _{c} a} \quad(a>0, \quad 且 a \neq 1 ; \quad c>0, \quad 且 c \neq 1 ; \quad b>0)$

三角函数

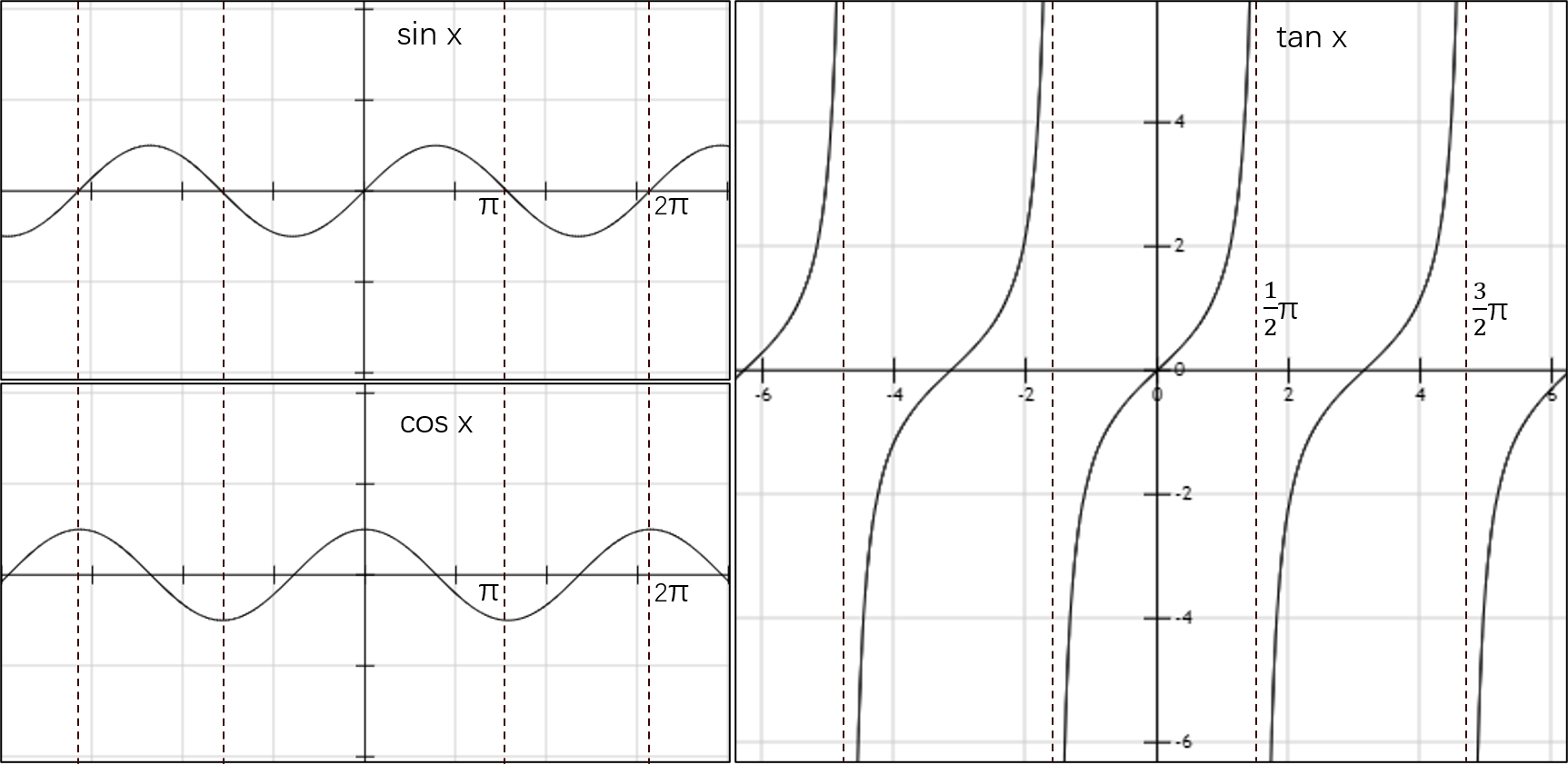
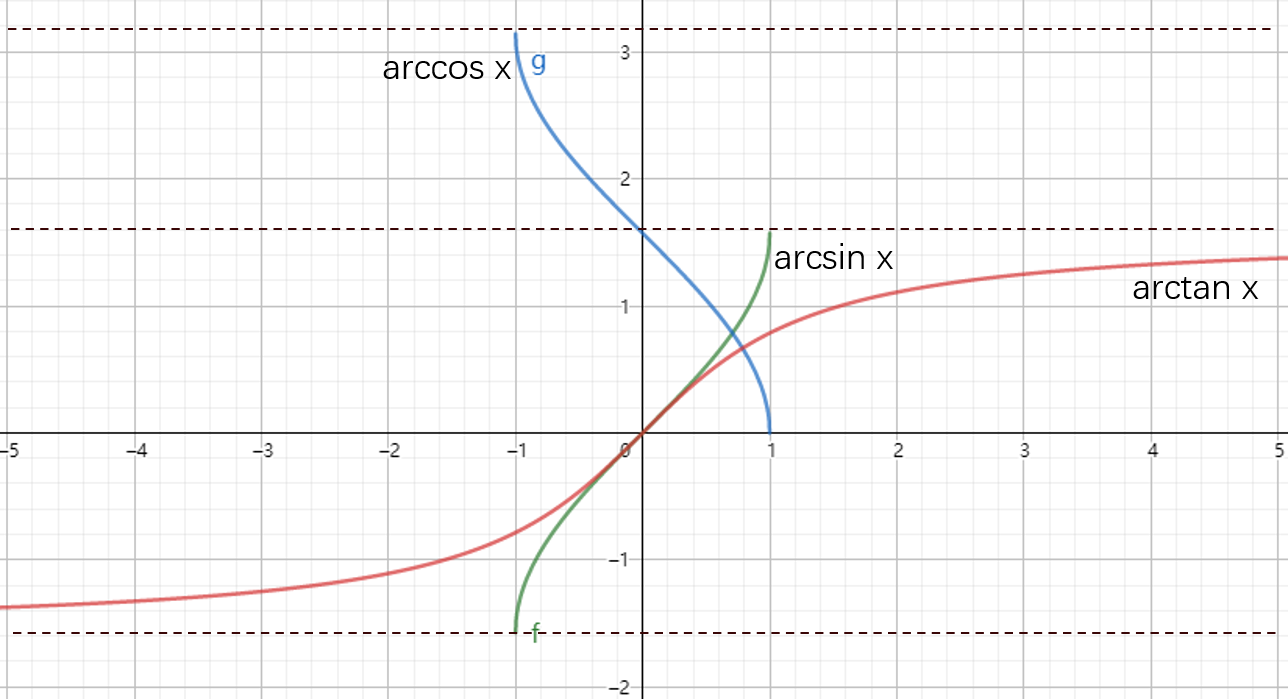
反三角函数

$\tan x=\frac{\sin x}{\cos x}$

$\cot x=\frac{\cos x}{\sin x}=\frac{1}{\tan x}$

$\sec x=\frac{1}{\cos x}$

$\csc x=\frac{1}{\sin x}$

诱导公式

$\sin ({2k\pi} +x)= \sin x$

$\cos ({2k\pi} +x)= \cos x$

$\tan ({k\pi} +x)= \tan x$

$\cot ({k\pi} +x)= \cot x$

$\sin (\frac \pi 2 +x)= \cos x$

$\cos (\frac \pi 2 +x)= -\sin x$

$\sin (\frac \pi 2 -x)= \cos x$

$\cos (\frac \pi 2 -x)= \sin x$

$\sin (\pi +x)= -\sin x$

$\cos (\pi +x)= -\cos x$

$\sin (\pi -x)= \sin x$

$\cos (\pi -x)= -\cos x$

$\sin (\frac {3\pi} 2 +x)= -\cos x$

$\cos (\frac {3\pi} 2 +x)= \sin x$

$\sin (\frac {3\pi} 2 -x)= -\cos x$

$\cos (\frac {3\pi} 2 -x)= -\sin x$

$tan(\frac \pi 2 + x)=－cot x$

$tan(\frac \pi 2－x)=cot x$

$cot(\frac \pi 2 + x)=－tan x$

$cot(\frac \pi 2－x)=tan$

$tan(\frac {3\pi} 2 + x)=－cotα$

$tan(\frac {3\pi} 2 －x)=cotα$

$cot(\frac {3\pi} 2 + x)=－tanα$

$cot(\frac {3\pi} 2 －x)=tanα$

平方关系

$\sin^2 x+\cos^2 x = 1$

$1+\tan^2 x = \sec^2 x$

$1+\cot^2 x = \csc^2 x$

两角和公式

$\sin (A+B)=\sin A \cos B + \cos A \sin B$

$\sin (A-B)=\sin A \cos B - \cos A \sin B$

$\cos (A+B)=\cos A \cos B-\sin A \sin B$

$\cos (A-B)=\cos A \cos B+\sin A \sin B$

$\tan (A+B)=\frac{\tan A+ \tan B}{1-\tan A \tan B}$

$\tan (A-B)=\frac{\tan A- \tan B}{1+\tan A \tan B}$

$\cot (A+B)=\frac{\cot A \cot B -1}{\cot A + \cot B}$

$\cot (A-B)=\frac{\cot A \cot B +1}{\cot A - \cot B}$

二倍角公式

$\sin 2a = 2 \sin a \cos a$

$\cos 2a = 2\cos^2 a - 1 = 1 - 2\sin^2 a = \cos^2 a - \sin^2 a = \frac{1 - \tan^2 a}{1 + \tan^2 a}$

$\tan2a = \frac{2\tan a}{1 - \tan^2 a} = \frac{2\cot a}{\cot^2 a - 1} = \frac{2}{\cot a - \tan a}$

$\cos^2a = \frac{1 + \cos 2a}{2}$

$\sin^2 a = \frac{1 - \cos 2a}{2}$

和差化积

$\sin a + \sin b = 2 \sin \frac{a + b}{2}\cos\frac{a-b}{2}$

$\sin a - \sin b = 2 \cos \frac{a + b}{2} \sin \frac{a-b}{2}$

$\cos a + \cos b = 2 \cos \frac{a + b}{2} \cos \frac{a - b}{2}$

$\cos a - \cos b = -2 \sin \frac{a + b}{2}\sin \frac {a - b}{2}$

$\tan a + \tan b = \frac{\sin (a + b)}{\cos a \cos b}$

$\tan a - \tan b = \frac{\sin (a - b)}{\cos a \cos b}$

$\cot a + \cot b = \frac{\sin (a + b)}{\sin a \sin b}$

$\cot a - \cot b = -\frac{\sin (a - b)}{\sin a \sin b}$

$\tan a + \cot b = \frac{\cos (a - b)}{\cos a \cos b}$

$\tan a - \cot b = - \frac{\cos (a + b)}{\cos a \cos b}$

积化和差

$\sin a \cos b = \frac{1}{2}[\sin(a + b) + sin(a - b)]$

$\cos a \sin b = \frac{1}{2}[\sin (a + b) - \sin (a - b)]$

$\cos a \cos b = \frac{1}{2}[\cos(a + b) + \cos(a - b)]$

$\sin a \sin b = - \frac{1}{2}[\cos(a + b) - \cos(a - b)]$

数集符号

符号	意义
N	非负整数集合或自然数集合{0,1,2,3,…}
N*或N+	正整数集合{1,2,3,…}
Z	整数集合{…,-1,0,1,…}
Q	有理数集合
Q+	正有理数集合
Q-	负有理数集合
R	实数集合(包括有理数和无理数)
R*	非零实数集合
R+/R-	正/负实数集合
C	复数集合
∅	空集(不含有任何元素的集合)